LE FastCounter
|
Feuillets plans de Riemann Hyperboloïde à une nappe Courbe en polaires Une convergence étrange |
|
|
Membre du Relais
Quelques jolies courbes
Les courbes de cette page ont été tracées à l'aide de MATLAB édité par The MathworksLes feuillets plans de Riemann
On supposera pour commencer que vous connaissez l'existance des nombres complexes (programme de terminale). Sinon, attachez vous principalement à l'aspect graphique des illustrations suivantes, l'objet de cette page n'étant pas de donner un cours magistral de mathématiques, mais plutôt d'éveiller votre intérêt pour la beauté naturelle de certaines courbes.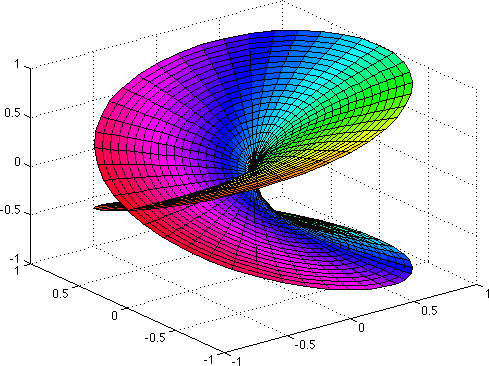
Commande MATLAB: cplxroot(2,20)
L'illustration ci-dessus est une visualisation de la racine carrée complexe. En effet, pour tout nombre réel x positif non nul, il existe deux réels dont le carré vaut x: ce sont x1/2 et -x1/2. On définit la racine carrée de x comme étant celui des deux qui est positif.
De la même manière, pour tout complexe z non nul, il existe deux complexes conjugués dont le carré vaut z. Mais il n'existe pas de relation d'ordre sur C. On ne peut donc en privilégier un des deux. C'est ce qui explique cette figure double: à chaque point du plan horizontal (plan complexe) correspondent deux racines.
On peut alors tracer la racine cubique complexe:
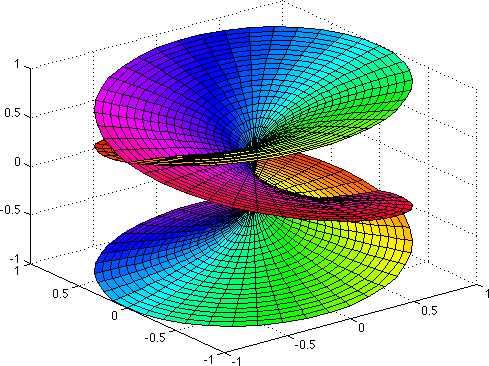
Commande MATLAB: cplxroot(3,20)
Cette fois, pour chaque complexe, on peut associer trois racines cubiques. En particulier, 1 possède trois racines cubiques distinctes dans C: 1, j et j2. (j=-1/2+i*31/2/2=ei 2Pi/3)
En poursuivant cette méthode, on peut tracer la racine n-ième complexe. Elle comporte n feuillets parallèles. Enfin, le logarithme complexe en possède lui une infinité. (On ne se risquera donc pas bien entendu à le tracer...)
Bibliographie: Théorie des fonctions de Georges Valiron (ed. MASSON)
Essayez aussi quelques-uns de mes liens vers les sites consacrés aux mathématiques.
Vos commentaires, questions, encouragements... à propos de cette page ou d'autre chose : cfranco@pobox.com
